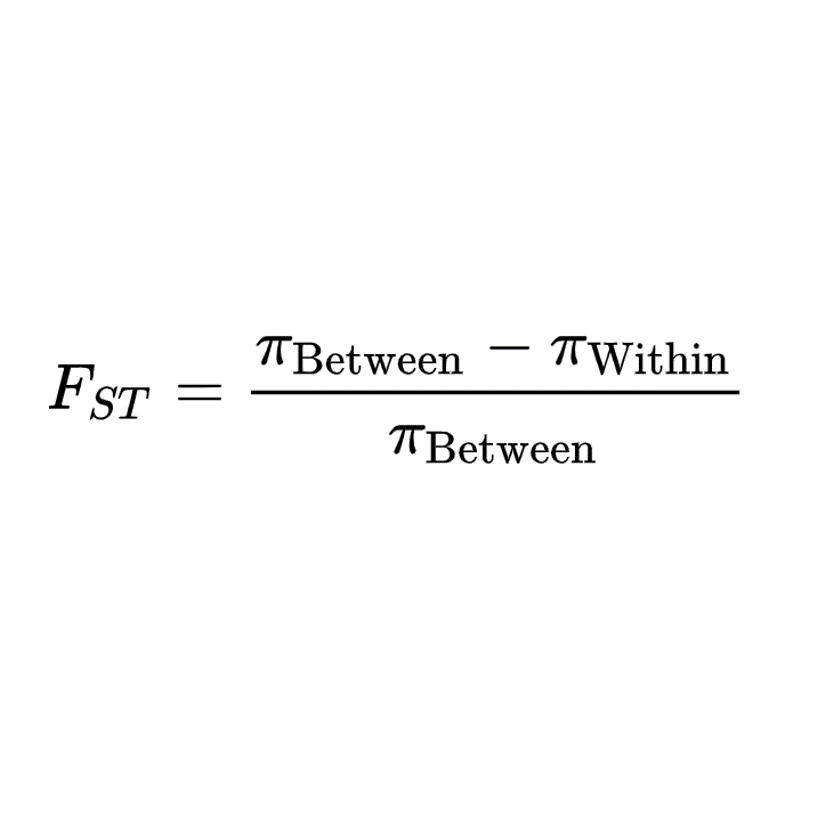
⬛ 정의
Fst란 F-statistics의 변형 형태 중 하나로, 집단 간 유전적 분화 정도를 비교할 때 사용된다
가장 흔하게 사용되는 정의는 1) 각 개체 간의 대립형질의 발현빈도(alle frequency)에 대한 분포(variance)를 기반으로 한 것과 2) 기원에 따라 일치(identical by descent, IBD)에 대한 확률을 기반으로 한 것이 있다.
Fixation index은 크게 3개로 볼 수 있다
- FST = Sub-population / Total
- FIS = Individual / Subpopulations
- FIT = Individual / Total
이중 가장 많이 쓰이는 FST를 보자
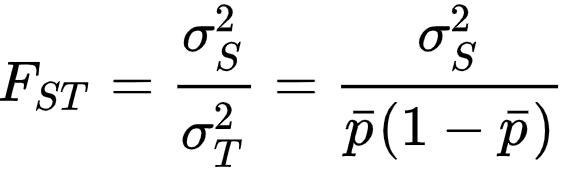
- p = 전체 개채의 대립유전자의 평균 발현 빈도
- σ_s = 다른 하위집단 사이의 대립유전지 빈도의 분산 값, 각 하위 집단의 수로 weigthed 된다(각 집단이 수가 영향을 미친다)
- σ_t = 전체 개채에 대한 대립유전자 상태에 대한 분산 값
⬛ 예시
값의 범위는 0~1이다.
이는 0에 가까울수록 두 집단 간 유전적 분화가 적어서, 거의 같은 종이라고 볼 수 있으며,
반대로 1에 가까우면 유전적 분화 정도가 크다고 볼 수 있음.
아래와 같이 동아시아(일본, 중국)와 아프리카(요루바), 유럽인들을 SNP단위로 유전자의 분화 정도를 비교한 표를 보자
| Europe (CEU) | Sub-Saharan Africa (Yoruba) | East-Asia (Japanese) | |
| Sub-Saharan Africa (Yoruba) |
0.153 | - | - |
| East-Asia (Japanese) |
0.111 | 0.190 | - |
| East-Asia (Chinese) |
0.110 | 0.192 | 0.007 |
가장 큰 Fst값은 0.192으로, 이를 보아 아프리카인과 동아시아(중국)인의 유전적 분화가 가장 크며,
가장 작은 0.007 값은 같은 동아시아인 중국 와 일본 사이의 값임으로 두 국가 간 유전적 분화는 이 중에서 가장 작다.
각 나라의 혼혈가족이 많은 유럽의 경우는 분화 정도가 더욱 적다.
| Italians | Palestinians | Swedish | Finns | Spanish | Germans | Russians | French | Greeks | |
| Palestinians | 0.0064 | ||||||||
| Swedish | 0.0064-|0.0090 | 0.0191 | |||||||
| Finns | 0.0130- 0.0230 |
0.0050- 0.0110 |
|||||||
| Spanish | 0.0010- 0.0050 |
0.0101 | 0.0040- 0.0055 |
0.0110- 0.0170 |
|||||
| Germans | 0.0029- 0.0080 |
0.0136 | 0.0007- 0.0010 |
0.0060- 0.0130 |
0.0015- 0.0030 |
||||
| Russians | 0.0088- 0.0120 |
0.0202 | 0.0030- 0.0036 |
0.0060- 0.0120 |
0.0070- 0.0079 |
0.0030- 0.0037 |
|||
| French | 0.0030- 0.0050 |
0.0020 | 0.0080- 0.0150 |
0.0010 | 0.0010 | 0.0050 | |||
| Greeks | 0.0000 | 0.0057 | 0.0084 | 0.0035 | 0.0039 | 0.0108 |
편차가 있는 값 이지만, 최댓값만 보았을 때 핀란드(Finns) 사람과 이탈리안 사람의 유전적 분화 정도가 제일 크며,
이탈리아 사람과 그리스(Greek) 사람의 유전적 분화도가 가장 작다.
⬛ 계산
그렇다면 어떻게 FST를 구하는가?
실제 예시와 함께 계산해보자
유전자형(genotype)이 AA, Aa, aa인 형질이 있다.
| AA | Aa | aa | total | |
| Subpopulation 1 | 125 | 250 | 125 | 1000 |
| Subpopulation 2 | 50 | 30 | 20 | 200 |
| Subpopulation 3 | 100 | 500 | 400 | 2000 |
각 하위그룹의 개체수는 다음과 같다
- Subpopulation 1 : 500
- Subpopulation 2 : 100
- Subpopulation 3 : 1,000
각 대립유전자는 유전자가 쌍으로 존재함으로 전체 유전자 빈도(= total)는 개체수 *2이다
📌 Step 1 : 대립유전자의 빈도 계산하기
여기서 A는 우성유전자, a는 열성 유전자라고 할 때,
각 집단이 가진 A 유전자의 빈도를 계산해보자
이때 Pn는 frequency of allele in population n를 뜻한다.
P1 = (2*125 + 250) / 1,000 = 0.50
P2 = (2*50 + 30) / 500 = 0.65
P3 = (2*100 + 500) / 2000 = 0.35
📌 Step 2 : 각 하위 그룹에서 하디-바인베르크 평형을 기반으로 예상되는 유전형의 빈도 계산
💡 하디-바인베르크 평형(Hardy-Weinberg Equilibrium)란?
이상적인 집단에서, 대를 거듭하더라도 유전자 풀에서 대립유전자의 빈도가 변하지 않고 평형상태를 유지하는 상태를 말한다.
예를 들어 각 유전형의 빈도가 A, a와 같을 때, n세대를 거친 유전자의 빈도는 아래와 같은 공식을 따른다
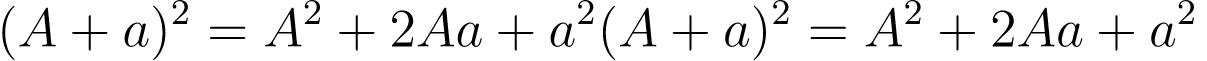
우리가 Step1에서 얻은 A의 빈도(p)는 P1에서 0.5, P2에서는 0.65, P3에서는 0.35였다. 이는 a가 나타날 빈도는 P1에서 0.5, P2에서는 0.35, P3에서는 0.65와 같다는 이야기(1-p임으로)이다. 아래와 같이 n세대가 지난 후의 각 유전자형의 기대 빈도를 계산해 보자.
| Pop. 1 | Expected AA = 500*0.5^2 | = 125 (= observed) |
| Expected Aa = 500*2*0.5*0.5 | = 250 (= observed) | |
| Expected aa = 500*0.5^2 | = 125 (= observed) | |
| Pop. 2 | Expected AA = 100*0.65^2 | = 42.25 (observed has excess of 7.75) |
| Expected Aa = 100*2*0.65*0.35 | = 45.5 (observed has deficit of 15.5) | |
| Expected aa = 100*0.35^2 | = 12.25 (observed has excess of 7.75) | |
| Pop. 3 | Expected AA = 1,000*0.35^2 | = 122.5 (observed has deficiency of 22.5) |
| Expected Aa = 1,000*2*0.65*0.35 | = 455 (observed has excess of 45) | |
| Expected aa = 1,000*0.35^2 | = 422.5 (observed has deficiency of 22.5) |
각 하위 그룹에서 하디-바인베트르크 평형일 때 동형접합을 정리해보자
- Pop. 1. 관찰값 = 기댓값 : 완전하게 동일하다
- Pop. 2. 동형접합이 기존 값에 비해 15.5 정도 초과했음 : 일부 inbreeding(근친교배)가 일어났음
- Pop. 3. 동형접합이 기존 값에 비해 45 정도 부족함 : 각 개체가 격리되어 교배가 일어나지 못함
📌 Step 3 : 각 하위 그룹에서 이형 접합체(heterozygosity)를 계산해라
관찰된 이형 접합체는 Hobs 라고 표시하겠다
이는 전체 population인구 대비 Aa의 수를 구하면 된다.
| AA | Aa | aa | total | |
| Subpopulation 1 | 125 | 250 | 125 | 1000 |
| Subpopulation 2 | 50 | 30 | 20 | 200 |
| Subpopulation 3 | 100 | 500 | 400 | 2000 |
- Hobs 1 = 250 / 500 = 0.5
- Hobs 2 = 30 / 100 = 0.3
- Hobs 3 = 500 / 1000 = 0.5
📌 Step 4 : 각 하위그룹에서 예측되는 이형 접합의 빈도를 계산해라
이는 Step2에서 계산한 값을 이용한다
| Expected | Observed | |
| Hexp1 = 1 - ∑(p₁² + p₂²) = 1 - (0.25 + 0.25) = 0.5 | = | 0.5 |
| Hexp2 = 1 - ∑(p₁² + p₂²) = 1 - (0.4225 + 0.1225) = 0.455 | > | 0.3 |
| Hexp3 = 1 - ∑(p₁² + p₂²) = 1 - (0.1225 + 0.4225) = 0.455 | < | 0.5 |
📌 Step 5 : 각 하위그룹의 inbreeding coefficient 계산하기
각 값은 (Hexp - Hobs)Hexp 값을 구하여라
- F1 = Hexp1 - Hobs1 = (0.5 - 0.5)/0.5 = 0
- F2 = Hexp2 - Hobs2 = (0.455 - 0.3)/0.455 = 0.341
- F3 = Hexp3 - Hobs3 = (0.455 - 0.5)/0.455 = -0.099
F>0 : 예상보다 적은 이형 접합체 = 근친교배(inbreeding)를 의미
F<0 : 예상보다 더 많은 이형접합체 = 과도한 이종교배(outbreeding)를 의미함
📌 Step 6 : 대립유전자 A의 빈도, p-bar 계산하기'
| AA | Aa | aa | total | |
| Subpopulation 1 | 125 | 250 | 125 | 1000 |
| Subpopulation 2 | 50 | 30 | 20 | 200 |
| Subpopulation 3 | 100 | 500 | 400 | 2000 |
(2*125+250 + 2*50 + 30 + 2*100+500) / (1000+200+2000) = 0.4156
📌 Step 7 : 대립유전자 a의 빈도, q-bar(= 1 - p)계산하기
( 2*125+250 + 2*20 + 30 + 2*400+500)/(1000+200+2000) = 0.5844
$$ \bar{p} + \bar{q} = 0.4156 - 0.5844 = 1 $$
📌 Step 8 : global heterozygosity indices 계산하기
Individuals, Subpopulations, Total population 간의 heterozygosity indices를 계산해보자
N은 각 하위그룹의 개체수를 의미한다
Hi = (Hobs1 * N1 + Hobs2 * N2 + Hobs3 * N3) / N_total
= (0.5*500 + 0.3*100 + 0.5*1000)/1600 = 0.4875
Hs = (Hexp1 * N1 + Hexp2 * N2 + Hexp3 * N3) / N_total
= (0.5*500 + 0.455*100 + 0.455*1000)/1600 = 0.4691
Ht = 1-∑(p² + q²) = 1- (0.4156^2 + 0.5844^2)= 1-(1.1727 + 0.3415) = 0.4858
= 혹은 2*p*q = 2*0.4156*5844 = 0.4858
📌 Step 9 : global F-STATISTICS 계산하기
FIS = (Hs - Hi) / Hs = (0.4691 - 0.4875) / 0.4691 = -0.0393
FIT = (Ht - Hi) / Ht = (0.4858 - 0.4875) / 0.4858= -0.0036
FST = (Ht - Hs) / Ht = (0.4858 - 0.4691) / 0.4858 = 0.0344
FIS는 이형접합체의 observed(관찰) 값을 기반으로 하며, FST는 이형접합체의 expected(기대) 값을 기반으로 한다
📌 Step 10: 계산한 값들을 정리해 보자
각 하위 그룹마다 total genetic variation은 약 3.4%이다(FST값).
FIT값이 0에 가까운 것을 보아. 전체 population에서 보았을 때 이형접합의 초과나 감소는 없다.
⬛ 기타
이는 보통 SNP 간의 차이를 보고 싶을 때 구하며, PLINK프로그램을 통해 쉽게 계산이 가능하다
프로그램 관련 글은 아래 위키에 적혀있다.
http://e.biohackers.net/F-statistics
⬛ Reference
(위키백과) https://en.wikipedia.org/wiki/Fixation_index
(계산법) http://www.uwyo.edu/dbmcd/popecol/maylects/fst.html
