풀이 날짜 : 2023-08-09(Python)

Pitfalls of Reversing Translation
연구자가 새로운 단백질을 발견할 때, 그들은 단백질에서 번역되어진 mRNA 서열을 추론한다. 이는 게놈에서 이 단백질과 관련된 위치한 유전자를 알아낼 수 있기 때문이다.
불행하게도, 어떠한 RNA 서열은 특별한 단백질 서열로 번역될 수 있지만, 그 반대 과정을 알아내려면 많은 그럼직한 RNA 서열을 유추해야 한다. 이는 하나의 단백질을 코딩하는데에 있어서 여러 RNA codon이 사용되기 때문이다.
일부 파이썬 버전에서는 int의 범위가 크지 않아서, 숫자를 저장하지 않고 조작하는 시스템을 고안해야 한다.
| Problem
모듈러 함수란?
8시에서 4시간이 지나면 2시로 표현하듯이, 각 값이 순환한 나머지 값을 말한다.
파이썬에서는 만약 x%n값이라면 n의 양/음수 배수에서 x축으로 얼마만큼 이동해야 x값이 되는지를 뜻한다.
물론 x축이 +, -값으로 이동하는 것 모두 수학적으로 옳지만, 파이썬의 경우 양의 방향으로 이동하는 값을 반환한다.
- ex) 7%3 = 1
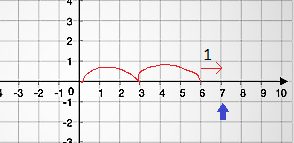
- ex) -7%3 = -2
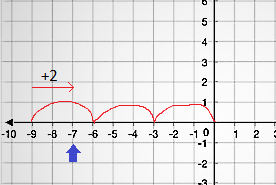
이를 mod로 표현하기도 한다.
만약 -10 mod 15는 5값을 말한다.
모듈러 함수의 특이점은 합동관계를 연관지을 수 있다.
a mod n=b mod n이라면, a = b mod n라고 할 수 있다
만약 -10 mod 15 = x라면 x mod 15 이다. 이때 x값은 어떤 값들이 될 수 있을까?
1) 먼저 -10 mod 15를 구한다. 이는 5값이다
2) 그렇다면 x mod 15도 5값을 가진다. 이때 x는 -25, 20등을 값으로 가진다.
이때 15에 해당하는 값을 modulo라고 한다. 이 문제에서는 modulo를 1,000,000값으로 잡을 것이다.
모듈러 함수란?
Given : 약 1000개의 amino acid 서열
output : 단백질로 번역될 수 있는 서로다른 RNA 문자열의 총 수 + 정지코돈을 간과하지 말자
| 예제 데이터와 결과
Sample Dataset
MASamplpe output
12M이 될 수 있는 코돈의 경우의 수 *A가 될 수 있는 코돈의 경우의 수 * 정지 코돈의 경우의 수 = 1*4*3 = 12
| Python
내 풀이
# 각 아미노산이 될 수 있는 코돈의 경우의 수
amino_acid_counts = {'I':3,'M':1, 'T':4, 'N':2, 'K':2,
'S':6,'R':6, 'L':6, 'P':4, 'H':2,
'Q':2,'V':4, 'A':4, 'D':2, 'E':2,
'G':4,'F':2, 'Y':2, 'C':2, 'G':4,
'W':1, 'stop':3}
stop_codon_num = 3
def possible_seq(protein_code) :
output = 1
for aa in protein_code:
output *= amino_acid_counts[aa]
output = output * stop_codon_num # 정지 코돈의 수를 곱해준다
return (output % 1000000) # 1000000수로 나눈 나머지를 결과값으로 내놓는다.
with open('./rosalind_mrna (4).txt', 'r') as f:
protein = f.read().strip()
print(possible_sequences(protein))
