- 수정 2023-03-22 : 오개념 수정
🟦 Alpha diversity란?
- Alpha diversity는 한 sample내의 종 다양성을 말한다. Alpha diversity를 이해하기 위해 아래 데이터를 사용해보자. 이 데이터는 한 바다에 5종의 생물이 발견되었음을 가정한다.
| Species | Number (n) | n(n-1) | p | pInp | p^2 |
| Sea holly | 2 | 2 | 0.1333333 | -0.26862 | 0.017769 |
| Sand couch | 8 | 56 | 0.5333333 | -0.33527 | 0.284409 |
| Sea bindweed | 1 | 0 | 0.0666666 | -0.18042 | 0.004436 |
| Sporobolus pungens | 1 | 0 | 0.0666666 | -0.18042 | 0.004436 |
| Echinophora spinosa | 3 | 6 | 0.2 | -0.32189 | 0.04 |
| Total | 15 | 64 | 1 | -1.2866 | 0.35105 |
- Number(n) : 해당하는 종이 몇 개체나 발견 되었는가
- p : 상대적인 풍부도, 각 값을 전체 대체의 수로 나눈다 = n/ total_number
그렇다면 이 바다가 다양성이 높다고 할 수 있을까? 이는 다양한 alpha diversity를 측정하는 지수, 지표로 부터 알 수 있다.
한 샘플에서의 다양도를 측정하는 지수는 다양도, 풍부도, 집중도, 균등도 등이 있다.
먼저 풍부도 지수 먼저 살펴보자.
🟦 Margalef 's Richness index , 종 풍부도 지수
- 가장 단순한 Richness는 가장 간단한 풍부도 지수로, 단순히 그 환경(샘플)에서 관찰된 종의 수(observed richness)를 말한다. 그러나 이는 종의 풍부도를 과소평가(각 종이 "얼마나" 존재하는지는 따지지 않음으로)하는 경향이 있다.
- 풍부도 지수 중 Margalef(1958)의 종 풍부도는 각 개체의 값으로 나누여 값을 표준화 해준다.
$$ R' = \frac{(S-1)}{Iog (N)} $$
- S : 종의 총 합
- N : 존재하는 개체의 합
위 예제 데이터에서 종의 풍부도 R'은 (5-1)/Iog(15) = 약 1.4771 값이다.
+) 또 다른 richness는 개체의 총 수를 고려하지 않고, 종의 총 수(즉 5값)만 가지는 지수도 있다.
🟦 Pielou's evenness index , 종 균등도 지수
- 종 균등조 지수는 단순히 종이 존재하는지 아닌지를 따지는 풍부도와 다르게, 그 종이 얼마나 존재하는지를 고려한다. 균등도는 여러가지가 있지만 일반적인 균등도는 Pielou’s evenness(1975)를 뜻한다. 이는 shannon diversity를 observed richness(풍부도)로 나눈 값이다.
$$ J' = \frac{H'}{H'_{max}} $$
H'는 shannon index를 말하며 H'max는 모두 비슷하다는걸 가정할 때H'값의 가능한 최대 값을 말하며 아래와 같다.
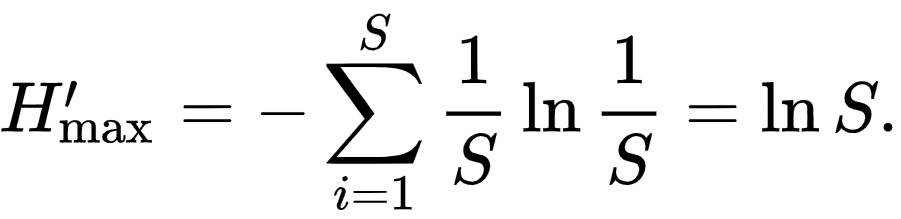
- S : 종의 총 수
$$ J' = \frac{H'}{In S}$$
위 예제데이터에서 Pielou의 균등도 값은 J'는 약 0.79940이다.
이 값은 0에서 1 사이값을 보이며, 값이 작을 수록 균등도가 높다.
🟦 Shannon-Wienner index , 종 다양도 지수(샤넌 지수)
$$ H' = - \sum^S_{i=1} p_i \textrm{in} p_i $$
- pi : i 번째 종 비율
- S : 군집의 종 수
한 종만 존재하면 S = 1, Pi = 1, 즉 H = 0, 0일 수록 종 풍부도가 낮다
위의 예시에서 shannon index는 1.2866이다
🟦 Simpson index , 종 집중도 지수(심슨 지수)
$$ D = \sum P_i^2 = \sum (\frac{n(n-1)}{N(N-1)}) $$
D는 0~1 값을 가지며, 클수록 다양성이 낮다
위 예시에서 D = 0.35105
🟦 Gini-Simpson = Simpson's index of diversity
$$ 1-D = 1 - \sum P_i^2 = 1- \sum (\frac{n(n-1)}{N(N-1)}) $$
0일 수록 다양성이 낮고 1일 수록 높다
위 예시에서는 1-D = 1- 0.35105 = 0.64895
🟦 Inverse Simpson index
$$ 1/D $$
위 예시에서는 1/D = 2.848597
🟦 faith's pd index 계통 다양도 지수
- 다른 다양성 지수와 다르게 Phylogenetic diversity(pd)는 sample 내 종의 계통적 정보도 고려하여 다양성을 따진다
간단하게 말하자면, Faith’s PD는 sample내의 모든 종의 branch length의 합산으로 계산된다
$$ PD' = \sum l(b) $$

한 sample에서 a, b, c, d, e가 관찰되고 PD는 각각의 branch length의 합을 말한다
즉 PD = 20+5+4+2+1+5+1+3 = 42이다
+)

+) 여러 index를 간편하게 계산해 주는 사이트
- https://virtue.gmbl.se/english-content/biodiversity-calculator
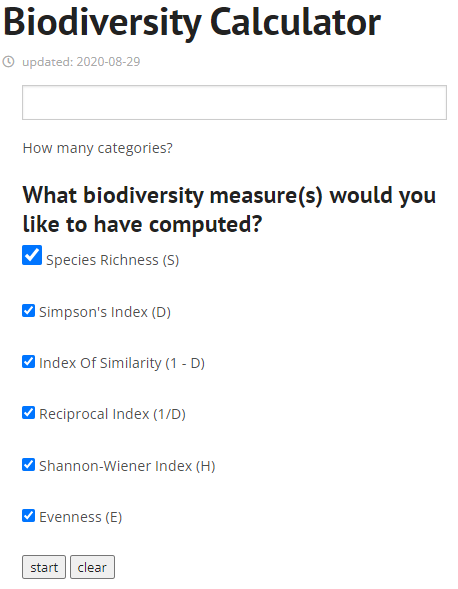
원하는 종의 수를 입력하고, 얻길 원하는 index를 체크한다 .
예시 데이터 입력 -> Start Analyses 클릭
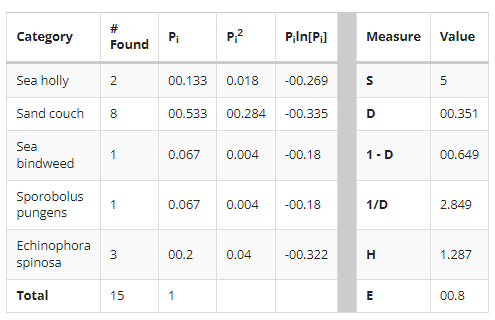
위 결과에서 다른 계산법을 사용한 eveness, richness 를 제외하고는 값이 동일하게 나온다.
🟦 Reference
- https://geographyfieldwork.com/Simpson'sDiversityIndex.htm
- https://en.wikipedia.org/wiki/Diversity_index#Simpson_index
- https://microbiome.github.io/OMA/alpha-diversity.html
- https://danielpfaith.wordpress.com/phylogenetic-diversity/
- Allen B, Kon M, Bar-Yam Y. A new phylogenetic diversity measure generalizing the shannon index and its application to phyllostomid bats. Am Nat. 2009 Aug;174(2):236-43. doi: 10.1086/600101. PMID: 19548837.
- 수학 공식 계산식 : https://www.codecogs.com/latex/eqneditor.php
- 수정 2023-03-22 : 오개념 수정
🟦 Alpha diversity란?
- Alpha diversity는 한 sample내의 종 다양성을 말한다. Alpha diversity를 이해하기 위해 아래 데이터를 사용해보자. 이 데이터는 한 바다에 5종의 생물이 발견되었음을 가정한다.
| Species | Number (n) | n(n-1) | p | pInp | p^2 |
| Sea holly | 2 | 2 | 0.1333333 | -0.26862 | 0.017769 |
| Sand couch | 8 | 56 | 0.5333333 | -0.33527 | 0.284409 |
| Sea bindweed | 1 | 0 | 0.0666666 | -0.18042 | 0.004436 |
| Sporobolus pungens | 1 | 0 | 0.0666666 | -0.18042 | 0.004436 |
| Echinophora spinosa | 3 | 6 | 0.2 | -0.32189 | 0.04 |
| Total | 15 | 64 | 1 | -1.2866 | 0.35105 |
- Number(n) : 해당하는 종이 몇 개체나 발견 되었는가
- p : 상대적인 풍부도, 각 값을 전체 대체의 수로 나눈다 = n/ total_number
그렇다면 이 바다가 다양성이 높다고 할 수 있을까? 이는 다양한 alpha diversity를 측정하는 지수, 지표로 부터 알 수 있다.
한 샘플에서의 다양도를 측정하는 지수는 다양도, 풍부도, 집중도, 균등도 등이 있다.
먼저 풍부도 지수 먼저 살펴보자.
🟦 Margalef 's Richness index , 종 풍부도 지수
- 가장 단순한 Richness는 가장 간단한 풍부도 지수로, 단순히 그 환경(샘플)에서 관찰된 종의 수(observed richness)를 말한다. 그러나 이는 종의 풍부도를 과소평가(각 종이 "얼마나" 존재하는지는 따지지 않음으로)하는 경향이 있다.
- 풍부도 지수 중 Margalef(1958)의 종 풍부도는 각 개체의 값으로 나누여 값을 표준화 해준다.
$$ R' = \frac{(S-1)}{Iog (N)} $$
- S : 종의 총 합
- N : 존재하는 개체의 합
위 예제 데이터에서 종의 풍부도 R'은 (5-1)/Iog(15) = 약 1.4771 값이다.
+) 또 다른 richness는 개체의 총 수를 고려하지 않고, 종의 총 수(즉 5값)만 가지는 지수도 있다.
🟦 Pielou's evenness index , 종 균등도 지수
- 종 균등조 지수는 단순히 종이 존재하는지 아닌지를 따지는 풍부도와 다르게, 그 종이 얼마나 존재하는지를 고려한다. 균등도는 여러가지가 있지만 일반적인 균등도는 Pielou’s evenness(1975)를 뜻한다. 이는 shannon diversity를 observed richness(풍부도)로 나눈 값이다.
$$ J' = \frac{H'}{H'_{max}} $$
H'는 shannon index를 말하며 H'max는 모두 비슷하다는걸 가정할 때H'값의 가능한 최대 값을 말하며 아래와 같다.
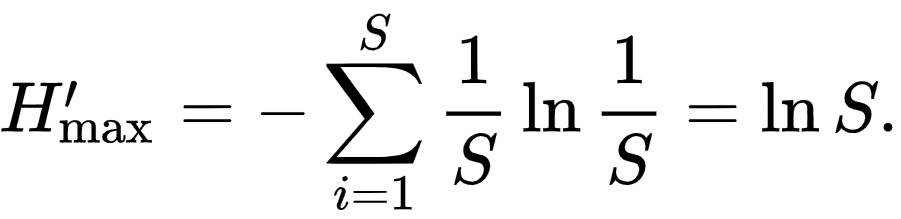
- S : 종의 총 수
$$ J' = \frac{H'}{In S}$$
위 예제데이터에서 Pielou의 균등도 값은 J'는 약 0.79940이다.
이 값은 0에서 1 사이값을 보이며, 값이 작을 수록 균등도가 높다.
🟦 Shannon-Wienner index , 종 다양도 지수(샤넌 지수)
$$ H' = - \sum^S_{i=1} p_i \textrm{in} p_i $$
- pi : i 번째 종 비율
- S : 군집의 종 수
한 종만 존재하면 S = 1, Pi = 1, 즉 H = 0, 0일 수록 종 풍부도가 낮다
위의 예시에서 shannon index는 1.2866이다
🟦 Simpson index , 종 집중도 지수(심슨 지수)
$$ D = \sum P_i^2 = \sum (\frac{n(n-1)}{N(N-1)}) $$
D는 0~1 값을 가지며, 클수록 다양성이 낮다
위 예시에서 D = 0.35105
🟦 Gini-Simpson = Simpson's index of diversity
$$ 1-D = 1 - \sum P_i^2 = 1- \sum (\frac{n(n-1)}{N(N-1)}) $$
0일 수록 다양성이 낮고 1일 수록 높다
위 예시에서는 1-D = 1- 0.35105 = 0.64895
🟦 Inverse Simpson index
$$ 1/D $$
위 예시에서는 1/D = 2.848597
🟦 faith's pd index 계통 다양도 지수
- 다른 다양성 지수와 다르게 Phylogenetic diversity(pd)는 sample 내 종의 계통적 정보도 고려하여 다양성을 따진다
간단하게 말하자면, Faith’s PD는 sample내의 모든 종의 branch length의 합산으로 계산된다
$$ PD' = \sum l(b) $$

한 sample에서 a, b, c, d, e가 관찰되고 PD는 각각의 branch length의 합을 말한다
즉 PD = 20+5+4+2+1+5+1+3 = 42이다
+)

+) 여러 index를 간편하게 계산해 주는 사이트
- https://virtue.gmbl.se/english-content/biodiversity-calculator

원하는 종의 수를 입력하고, 얻길 원하는 index를 체크한다 .
예시 데이터 입력 -> Start Analyses 클릭

위 결과에서 다른 계산법을 사용한 eveness, richness 를 제외하고는 값이 동일하게 나온다.
🟦 Reference
- https://geographyfieldwork.com/Simpson'sDiversityIndex.htm
- https://en.wikipedia.org/wiki/Diversity_index#Simpson_index
- https://microbiome.github.io/OMA/alpha-diversity.html
- https://danielpfaith.wordpress.com/phylogenetic-diversity/
- Allen B, Kon M, Bar-Yam Y. A new phylogenetic diversity measure generalizing the shannon index and its application to phyllostomid bats. Am Nat. 2009 Aug;174(2):236-43. doi: 10.1086/600101. PMID: 19548837.
- 수학 공식 계산식 : https://www.codecogs.com/latex/eqneditor.php
