작성 : 2022-11-28
수정 : 2023-03-21

🟥 Beta diversity란?
마이크로 바이옴의 기본 분석 단계는 아래와 같다.
1. alpha diversity → 2. beta diversity → 3. Taxonomy composition
이 중 beta diversity는 각 샘플 간의 다양성을 비교하는 방법이다.
이는 데이터 분석 단계의 clustering(군집분석)에 해당하며, 생물학적 군집을 비교(clustering)할 때 뿐만 아니라 여러 데이터 분석에서도 쓰이는 단계이다.
Beta diversity에 쓰이는 거리 계산 방법은 크게 두 부류로 나눌 수 있다.
Qualitative vs. Quantitive diversity
| 질적(qualitative) 다양성
- read의 양으로 sequence abundance를 판별한다. 관련 지수로는 Bray-Curtis, weighted Unifrac가 있다.
| 양적(quantitive) 다양성
- 그 서열(여기서는 feature*)이 있는지 없는지 판별한다. 관련 지수로는 Binary Jaccard, unweighted Unifrac가 있다.
* 여기서 feature란 OTU, ASV를 말하며, 분류되는 amplicon 분석에서 marker gene(16S, 18S, ITS .. )들이 군집화된 단위를 말한다.
Based Phylogenetic tree vs. Not
| Phylogenetic diversity
- taxa 간의 evolutionary relationship고려한다. 관련 지수는 Unifrac 등 이 있다.
| Non-phylogenetic diversity
- evolution 하게 관련 없다고 가정하여 모든 taxa가 동일한 relationship을 가진다. 종류는 Bray-Curtis와 Jaccard가 있음
일단 기본 개념인 유사도부터 알아보자
🟥 유사도(Similarity)란?
유사도(Similarity)란? 두 데이터가 얼마나 비슷한지 측정하는 척도
일반적으로 0과 1 사이의 값을 가진다.
비유사도(Dissimilarity)란? 두 데이터가 얼마나 다른지 측정하는 척도
0에서 무한대의 범위를 가진다.
유사도(s)와 비유사도(d)는 아래와 같은 관계를 같는다.
d = 1- s
📌 거리(Distance)와 유사도(silmilarity)의 차이
그렇다면 거리와 유사도는 다른 개념인가?
- The answer to “How far apart are these points?” (얼마나 멀리 떨어져 있나? ) is their distance
- The answer to “How close together are these points?”(얼마나 가까이 있나?) is their similarity
즉 distance는 silmilarity보다 dissilmilarity(얼마다 유사하지 않은가)와 개념이 더 유사하다.
📌 1차원 변수의 유사도 측정법(x~y사이의 거리)
| 속성 유형 | 비유사도 | 유사도 |
| 명목형 (nominal) |
if x = y, d = 0 if x != y, d = 1 같으면 0, 다르면1 |
if x = y, s = 1 if x != y, s = 0 같으면1,다르면0 |
| 서열형 (ordinal) |
d = |x - y| / ( n - 1) (속성의 값이 n개인 경우) |
s = 1 - d |
| 숫자형 (numeric = Interval / Ratio ) |
d = |x - y| | s = -d, s = 1 / (1 + d) 등 |
- 명목형의 경우 계체의 동일여부만 확인, 두 속성값이 동일하다면 -> 유사도는 1
- 서열형 : n-1로 나누는 이유는 속성값의 개수에 관계없이 동등한 구간 유지를 위함
- 숫자형 : 산술연산이 가능함으로 단순히 |x-y|로 계산한다
📌 다차원 변수의 유사도 측정법
크게 거리(Euclidean distance..) 기반과 각도기반(cosine similarity..)으로 나눌 수 있다.
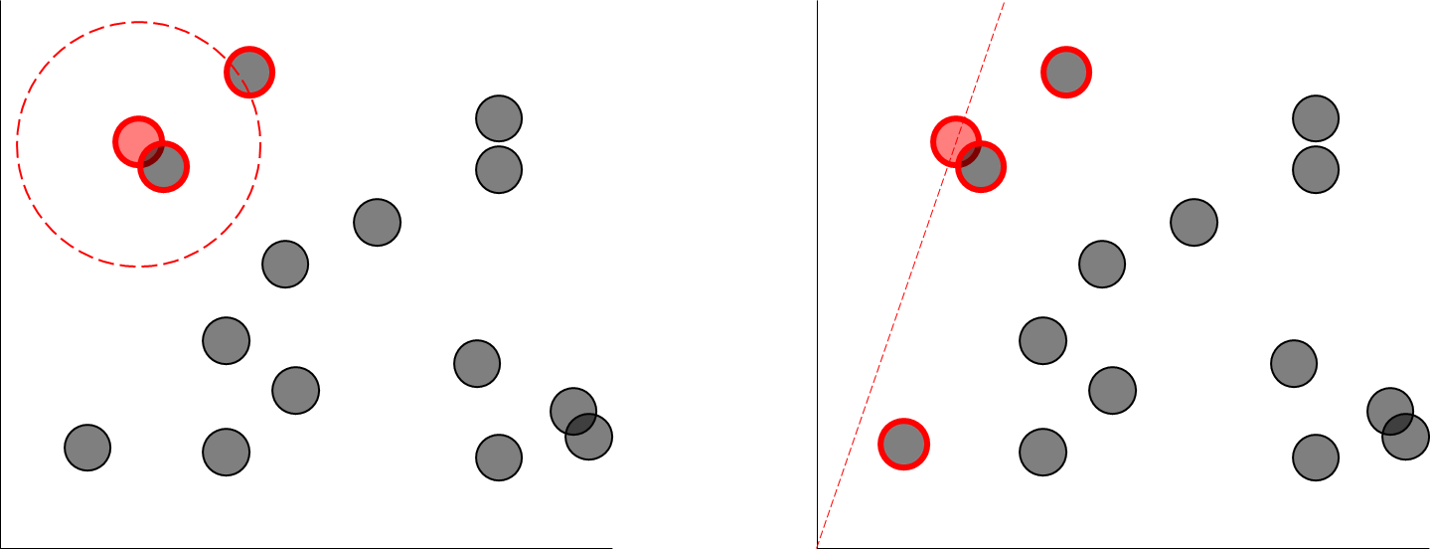
1) Euclidean Distance
두 점간의 최소 직선사이의 거리를 말한다. 이는 피타고라스 정리를 이용한다.

2차원 공간에서 두 점간의 거리는 아래와 같다
D(X, Y) = √((x1-x2)^2 + (y1-y2)^2)
또한 n차원에서 유클리드 거리는 아래와 같다
d(p,q)=√ (p1−q1)2+(p2−q2)2+...+(pn−qn)2
2) Manhattan Distance
taxicab geometry 등으로 불리며, 맨해튼 도시의 직선거리와 비슷하다고 하여 붙여진 이름이다.
아래 예시와 같이 형광초록색(Euclidean Distance)을 제외한 모든 거리는 Manhattan distance(모두 같은 값)에 속한다.
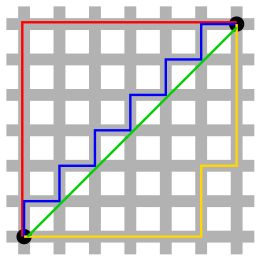
두 점사이의 거리는 아래와 같다
D(X, Y) = |x1-x2| + |y1-y2|
3) Minkowski distance
맨해튼 거리와 유클리드 거리가 하나의 공식으로 포함된 식이다
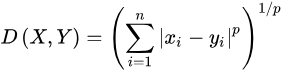
n = 각 차원
만약 p=1이면서, n = 2(2차원) 일 때, 각 절댓값의 차이이며 이는 맨해든 거리와 동일 = L1 norm
p = 2이면, 유클리드와 비슷하다. = L2 norm
p = ∞ , chebyshev dstance와 동일 = L max norm이라고 한다
4) Cosine Similarity
두 벡터의 크기가 아닌 방향성의 차이만 판단한다.
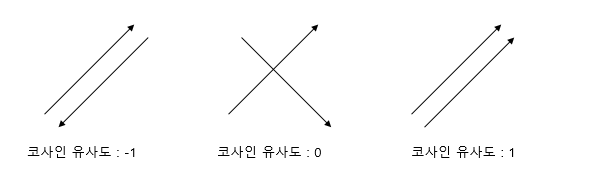
두 백터가 이루는 각이 작을수록 유사도가 높고, 값은 1에 가깝
각이 클수록 유사도가 작고, 이 값은 -1에 가깝다.
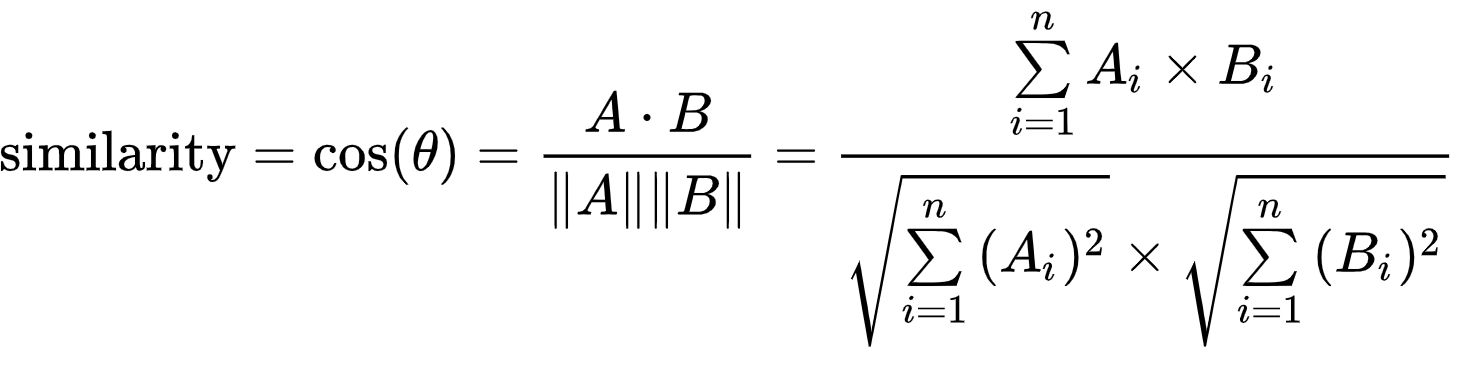
계산은 두 백터의 내적을 각 벡터의 norn(백터의 크기)의 곱( = ||A||*||B||)으로 나눈다.
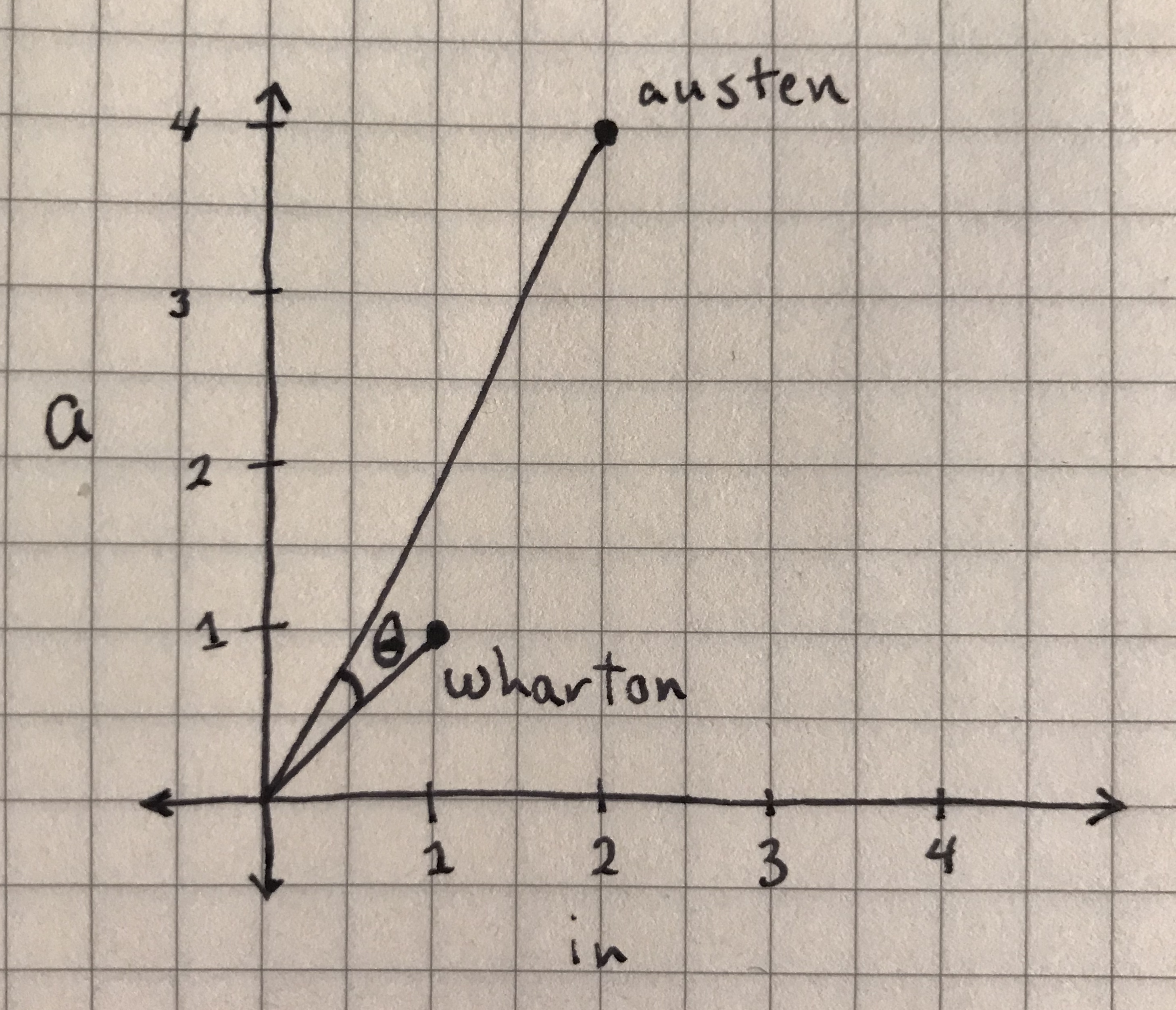
즉 두 벡터 간 거리가 멀어도 각도가 같다면 유사하다고 볼 수 있다.
사실 Mahalanobis distance 등등 여러 거리 계산법이 존재한다.
이들은 파이썬의 scipy 이 모듈에서 쉽게 계산가능하며,
[초심자를 위한 생물학+정보학] 다양한 거리 계산 - 37( https://www.ibric.org/myboard/read.php?Board=news&id=272298 )에서 여러 거리를 볼 수 있다.
+) distance의 차이로 분석하면 나누면 차원의 저주 때문에 성능저하가 일어남으로, 차원축소 기법(PCA, PCoA, NMDS...)으로 분석한다.
참고 1 : 차원의 저주
🟥 Dissimilarity in Beta diversity
자 이제 마이크로바이옴 분석에 많이 쓰이는 distance, dissimilarity를 분석해 보자. (이전에 Dissimilarity의 범위는 보통 무한이라고 언급했지만, 여기서는 값의 정의가 다르다)
만약 아래와 같은 3개의 생물이 i, j환경에서 발견되었다고 가정해 보자.
| Sample i | Sample j | |
| A Species | 6 | 10 |
| B Species | 7 | 0 |
| C Species | 4 | 6 |
📌 Bray-Curtis Dissimilarity
J. Roger Bray와 John Thomas Curtis가 만든 지수로, 생물학과 환경분야에서 두 지역의 비유사성을 판단하는 지표로 사용된다. bray curtis값의 범위는 총 0에서 1 사이로, 0에 가까울수록 두 샘플의 종 구성이 같다는 뜻이다.
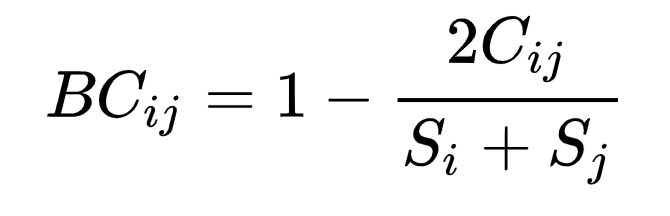
사이트 i와 j에 대해서 본다면.
- C_ij : 각 사이트에서 공통적으로 나타난 종의 공통적인 수
- S_i : i에서 나타나는 종의 총 합
- S_j : j에서 나타나는 종의 총 합
| Sample i | Sample j | |
| A Species | 6 | 10 |
| B Species | 7 | 0 |
| C Species | 4 | 6 |
각 sample에서 공통저인 종은 A와 C이며, 각 공통적인 종의 최소 수를 더한 값이 C_ji이다. 이를 계산하면 아래와 같다.
C_ji = 6(A specie)+4(C specie) = 10
S_i = i 사이트의 각 종의 수의 합 = 6 + 7 + 4 = 17
S_j = 10 + 6 = 16
임으로 bray-curtus 값을 계산해 보면1-(2*10)/(17+16) = 0.39 값이다.
미생물 분석에서는 reletive distance값이 쓰임으로 실제계산은 이와 다를 수 있다.
📌 Jaccard Dissimilarity, Jaccard distance
Jaccard similarity란 Paul Jaccard가 개발한 지수로, 주로 환경샘플에서 각 지역에서 샘플 간의 다양성을 측정할 때 사용한다. 두 지역의 합집합 대비 교집합 비율을 나타낸다.
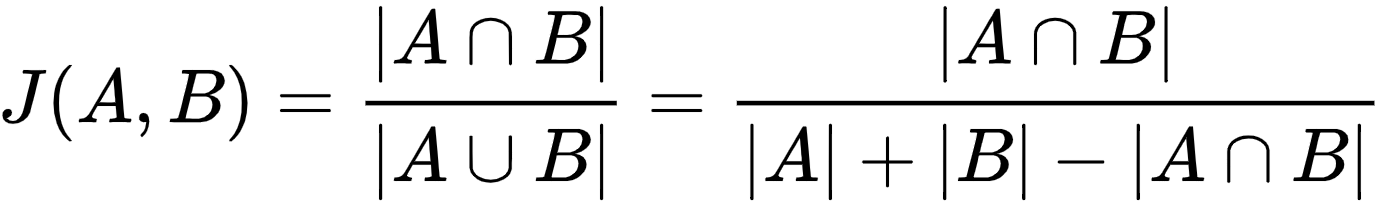
jaccard 유사도의 범위는 1에서 0 사이로, 0에 가까울수록 두 그룹은 교집합 하는 종이 적음으로 유사하지 않다.
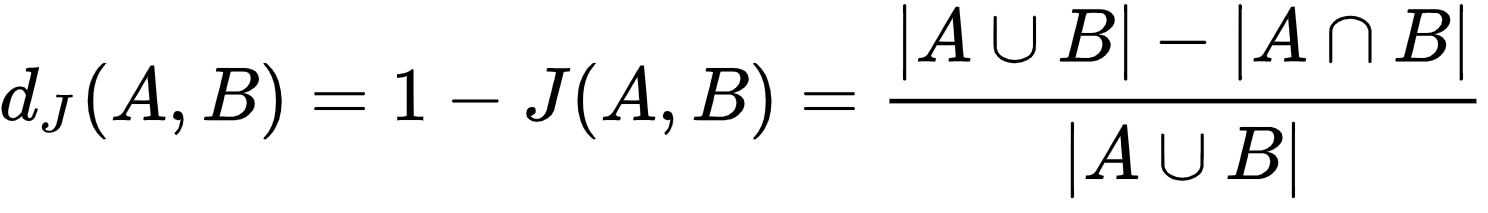
jaccard 비유사도의 범위는 0에서 1 사이로, 0에 가까울수록 두 그룹은 유사하다.
jaccard는 각 종의 수(미생물 데이터에서는 read count)를 기반으로 하는 것이 아니라, 각 종이 그룹에 존재하는지 아닌지를 기반으로 한다.
| Sample i | Sample j | |
| A Species | 6 | 10 |
| B Species | 7 | 0 |
| C Species | 4 | 6 |
만약 site i와 j가 위와 같다면,
i∪j = (A, B, C) = 3,
i∩j = (A, C) = 2, 이므로 | i∪j | - | i∩j | = 1이다.
그러므로, Jaccard dissimilarity = 1- (1/3) = 0.6666이다.
📌 Unifrac Distance
Unifrac은 Catherine Lozupone에 의해 고안되었으며 계통유전학적 서열 간의 거리(branch length)를 이용한다. Unifrac은 Jaccard처럼 공통된 종의 유무만 따지는 unweighted Unifrac과, 각 종의 abundance정보를 추가한 weighted Unifrac이 있다.
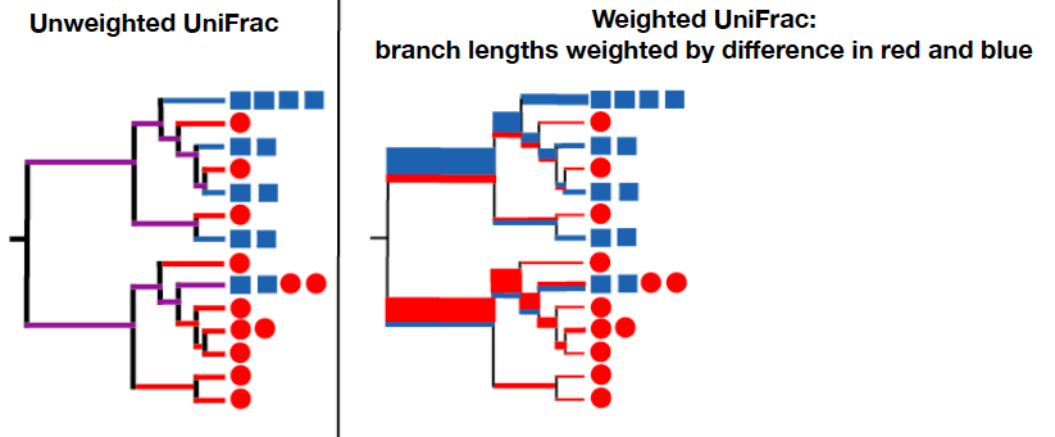
| Unweighted Unifrac 계산 방법
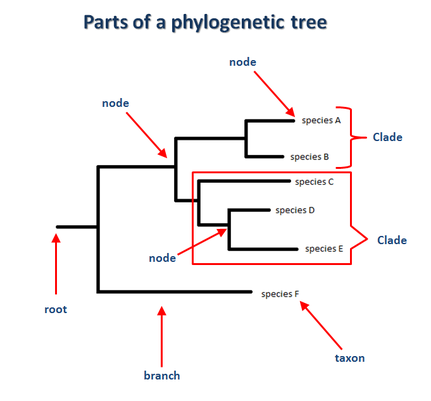
실제 계산 공식은 아래와 같다
N = the number of nodes(=OTU) in the tree
i = node
l = the branch length between node
Ai = A그룹에 존재하면 1, 아니면 0
Bi = B그룹에 존재하면 1, 아니면 0
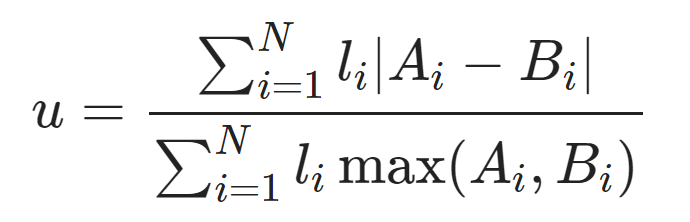
결과적으로 각 그룹 내에 여러 종(OTU)이 비슷한 abundance로 존재한다면 D = 0이며.
각 tree와 각 그룹이 잘 그룹 지어진다면 이는 1 값을 가진다.
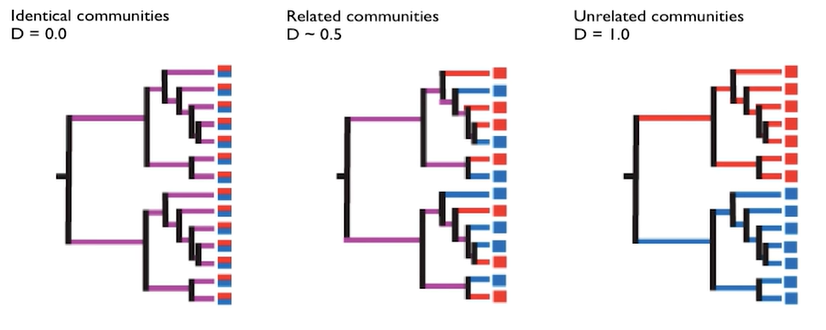
아래 예제 사진으로 다시 한번 개념을 떠올려보자.
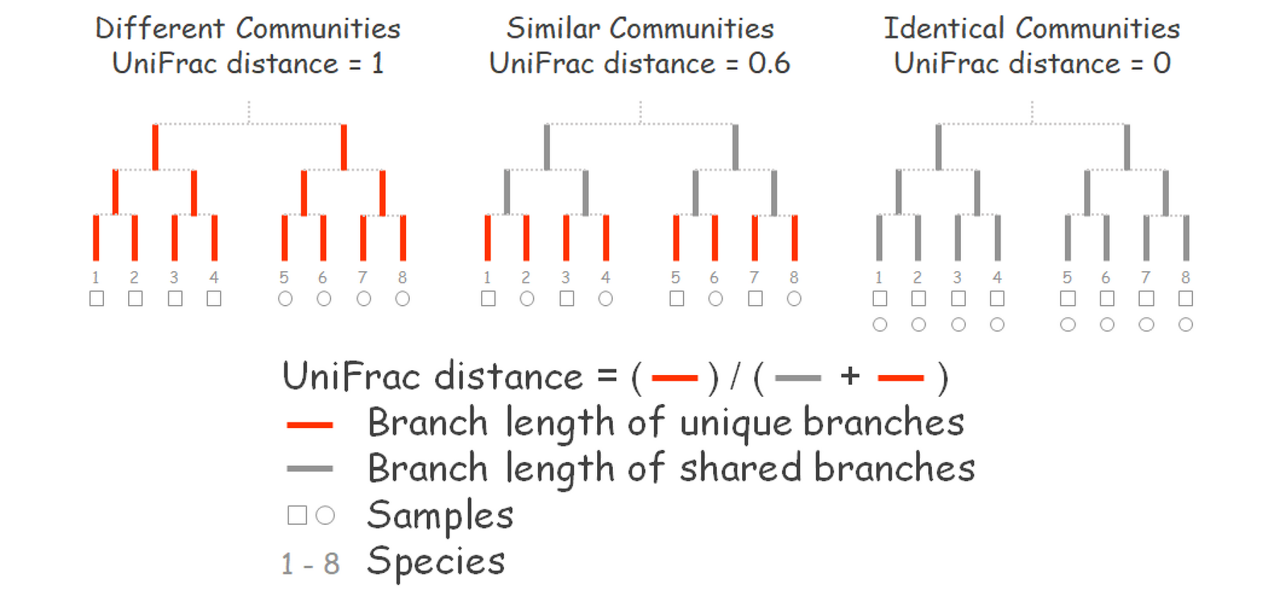
- 맨 왼쪽의 그림은 각 □, ○ 샘플에서 계통적으로 거리가 먼 생물들이 서로 다른 샘플에서만 출현하였다. 이때 Unifrac의 거리는 1이며 이는 각 샘플마나 공유하는 생물이 존재하지 않는다는 의미이다.
- 가운데 그림은 □, ○ 샘플에서 계통적으로 가까운 생물들이 존재하는 것을 볼 수 있다. 이때 각 샘플에서만 Unique 한 branch의 개수는 8, 두 샘플이 공유하는 계통수의 branch는 6이다. 이를 Unifrac distance로 바꾸면 8/(6+8) = 0/5714.. 이 된다.
- 맨 오른쪽 그림은 모든 샘플에서 모든 종을 공유하고 있는 상황이다. 이때 Unifrac의 값은 0이며, 두 샘플의 관계가 아주 가깝다는 것을 의미한다.
+) 3개의 샘플일 경우 Unifrac으로 beta diversity계산
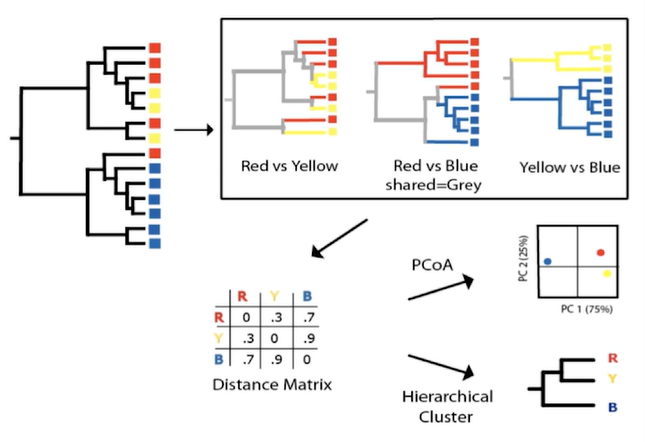
- 계통수의 14개의 정사각형은 OTU를 뜻하며 그 OTU가 어떤 샘플에 포함되어 있는지를 색으로 구분해 주었다. 이때 우리가 보고 싶은 것은 3개의 그룹이 가까운지 아닌지 distance로 나타내고, 이를 PCoA로 시각화해 주는 것이다.
- 방법은 아래와 같다
1) red-yellow-blue 각 그룹을 pairwise(짝지어서 비교)로 비교 distance matrix로 정리하고
2) 이 distance를 이용하여 PCoA를 그리거나 계층적 cluster로 묶는다.
그러다 계통수는 여러 종류로 묶일 수 있기 때문에 아래와 같이 랜덤 하게 계통수를 만들어 여러 번 계산한다.
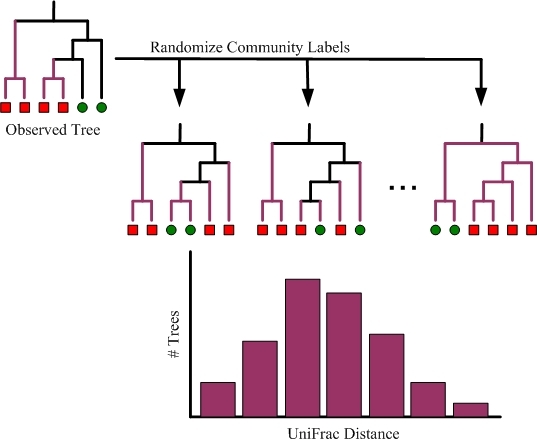
| Weighted Unifrac 계산 방법
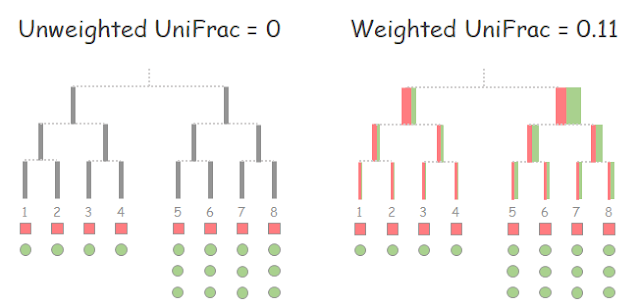
샘플에서의 각 종의 유무와, 그 종이 얼마나 풍부하게 있는지(여기선 계통수의 branch의 굵기로 표현)를 고려한 지수이다.
🟥 정리하자면..
bray curtis는 각 종(OTU)의 read count나 abundance를 기준으로 각 그룹(sample)의 거리 계산
jaccard는 그 종(OTU)이 각 sample에 있는지 여부로 계산
Unifrac은 OTU 간의 계통수를 그려보고, 그룹에 맞게 계통수도 잘 나누어지는지 본다.
🟥 Reference
- https://programminghistorian.org/en/lessons/common-similarity-measures
- https://m.blog.naver.com/parkjy76/220102695206
- https://www.youtube.com/watch?v=ofIfXMPem2M
- https://en.wikipedia.org/wiki/Euclidean_distance
- https://www.ibric.org/myboard/read.php?Board=news&id=271138&BackLink=L215Ym9hcmQvbGlzdC5waHA/Qm9hcmQ9bmV3cyZQQVJBMz0xMA=
- https://ko.wikipedia.org/wiki/%EC%BD%94%EC%82%AC%EC%9D%B8_%EC%9C%A0%EC%82%AC%EB%8F%84
- https://en.wikipedia.org/wiki/Bray%E2%80%93Curtis_dissimilarity
- https://www.metagenomics.wiki/pdf/taxonomy/alpha-beta-diversity
- https://www.youtube.com/watch?v=M8ylvsS0MHg
- https://www.quora.com/What-is-the-easiest-way-to-define-the-UniFrac-distance
- https://mothur.org/wiki/unweighted_unifrac_algorithm/
- https://qcb.ucla.edu/wp-content/uploads/sites/14/2017/12/QCB_W11-Metagenomics-Analysis_BS_day3.pdf
- https://forum.qiime2.org/t/unweighted-vs-weighted-unifrac-explanation/2206/6
