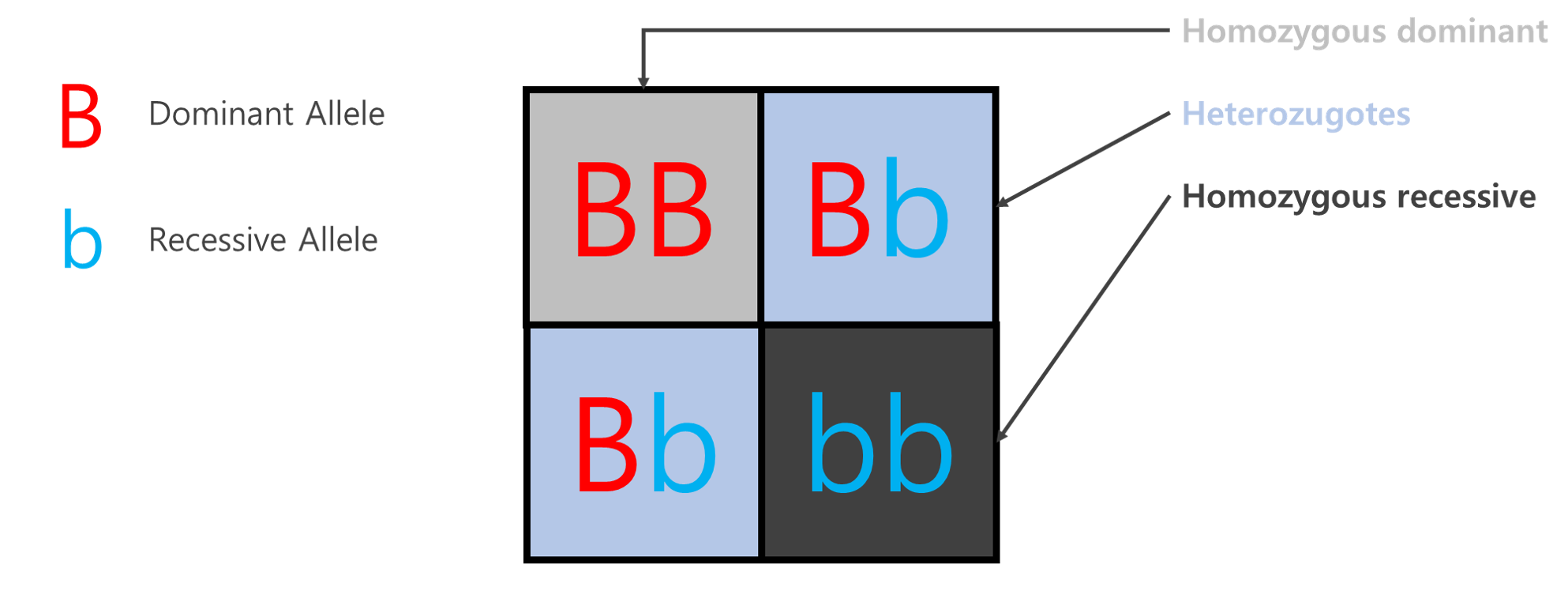
우열의 법칙 : 제1대 잡종에서 대립형질중에 우성형질만 나타난다.

문제
멘델의 법칙이란 다들 알고 있으니 설명은 건너뛰고 문제 풀이부터 가겠다
일단 문제는 BB, Bb가 몇의 확률로 나타날 수 있다는 것이다
Sample Dataset
주어지는 sample데이터는 아래와 같다
2 2 2Sample Output
0.78333
Input data의 첫 자리는 k, 가운데는 m, 마지막은 n 형의 개체군의 각 수를 뜻하는데,
k는 homozygous dominant(BB), m은 heterozygous(Bb), n은 homozygous recessive(bb)를 말한다
즉 2 2 2 는 k, m, n의 유전자형을 가진 개체가 2 마리씩 존재한다.
이 개체군에서 dominant allele(BB, Bb) 즉 우성 표현형을 나타내는 개체를 생산할 확률을 구하는 것이다
일단 k=2, m=2, n=2일때 교배 가능한 경우의수는 BBXBB, BbXBb, bbXbb, BBXBb, BBXbb, BbXbb가 있다
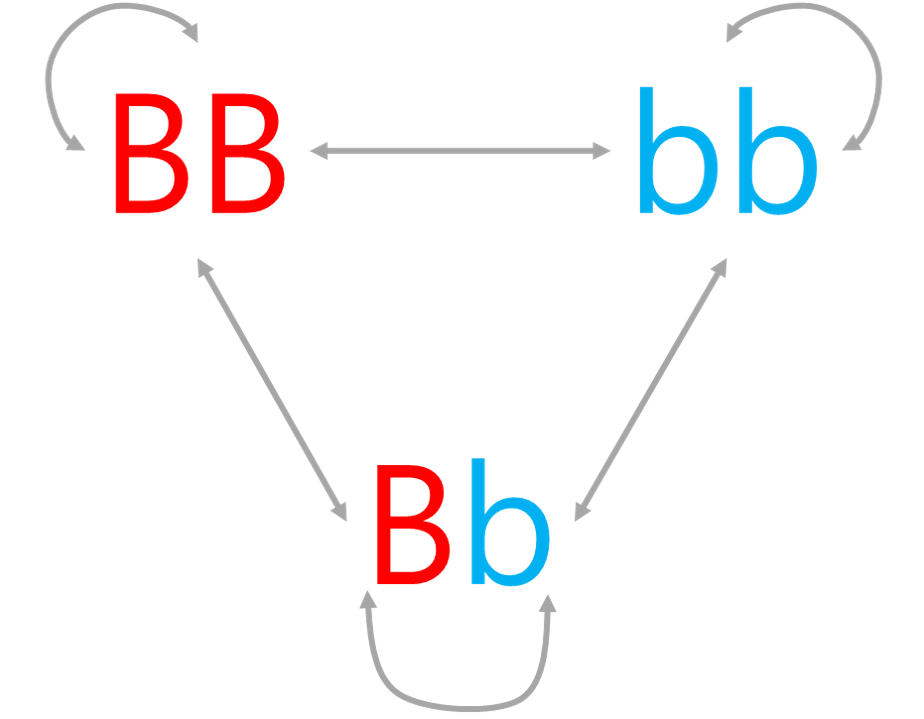
전체 확률변수의 합은 1이다.
간단하게 생각하면 여기서 bb가 생길 확률을 제거하면 된다.
각 자손형에서 bb가 나올 확률을 보자
BBXBB의 자손형은 BB, BB,BB, BB → 여기서 bb는 0/4
BbXBb의 자손형은 BB,Bb,Bb,bb → 여기서 bb는 1/4 → (1)
bbXbb의 자손형은 bb,bb,bb,bb → 여기서 bb는 4/4 → (2)
BBXBb의 자손형은 BB,BB,Bb,Bb → 여기서 bb는 0/4
BBXbb의 자손형은 Bb,Bb,Bb,Bb → 여기서 bb는 0/4
BbXbb의 자손형은 Bb,Bb,bb,bb → 여기서 bb는 2/4 → (3)
여기서 bb가 나올 경우의 수((1), (2), (3))는 아래와 같다


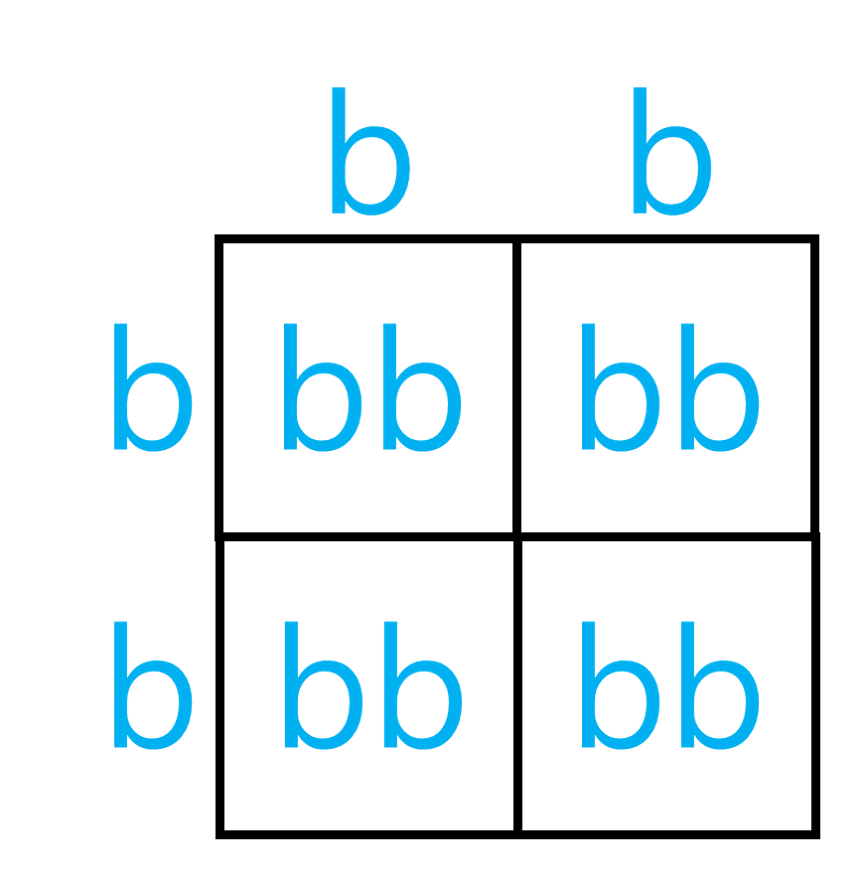
일단 교배 확률 구하는 법을 생각해 보자
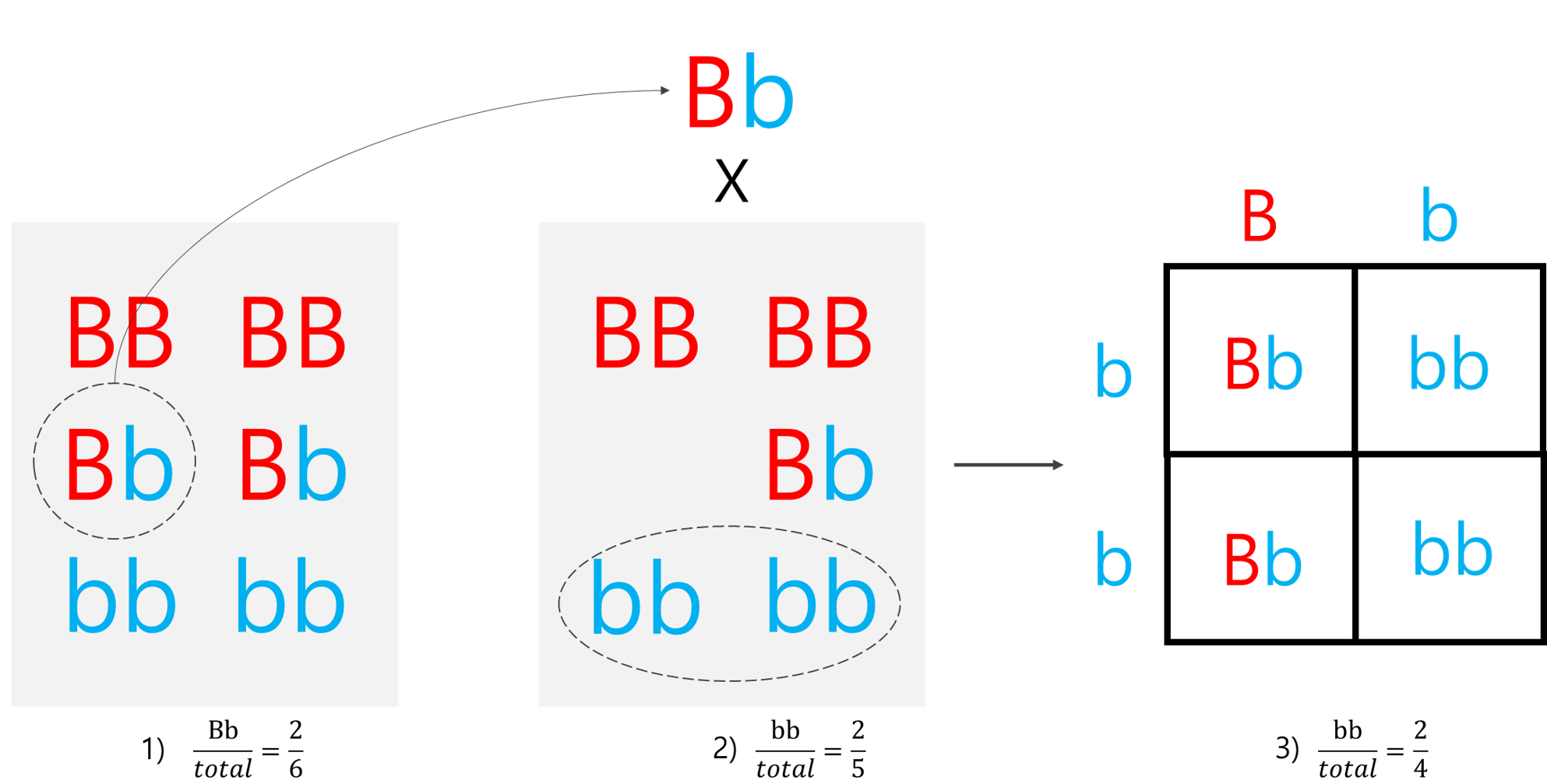
예를들어 (1) BbXBb의 교배 확률을 구한다면 어떻게 구해야 할까?

1) 처음에 Bb는 2/6확률로 존재하며
2) 그 다음 Bb는 1/5확률로 존재한다.
→ BbX Bb의 교배에서 bb가 나올 확률은 2/4이므로, 2/6*1/5*1/4 = 1/60이다
(2) bbXbb의 교배 확률을 구한다면 어떻게 구해야 할까?
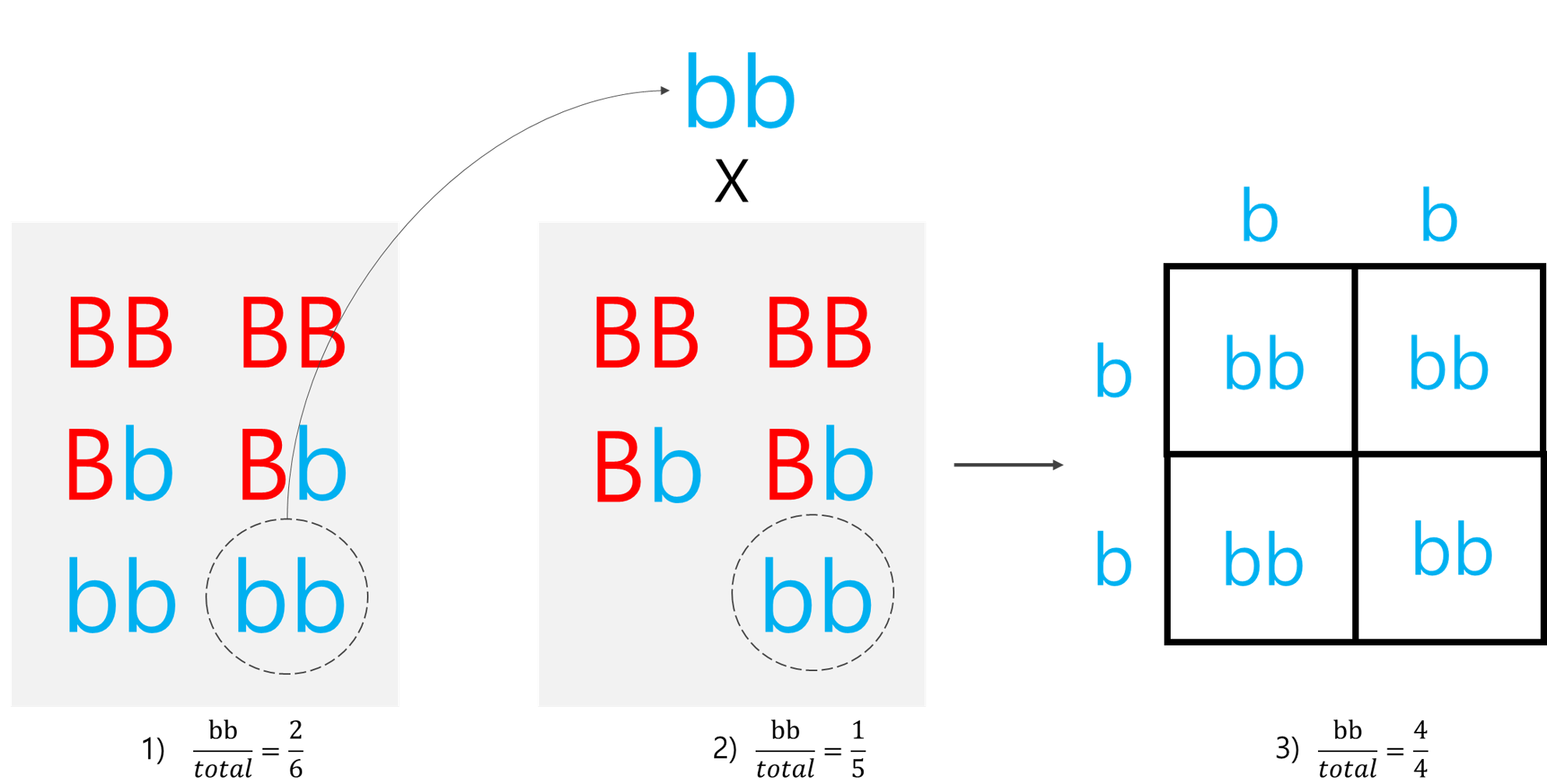
1) 처음에 bb는 2/6확률로 존재하며
2) 그 다음 bb는 1/5확률로 존재한다.
→ bbXbb의 교배에서 bb가 나올 확률은 2/4이므로, 2/6*1/5*4/4 = 4/60이다
(3) BbXbb의 교배 확률은?
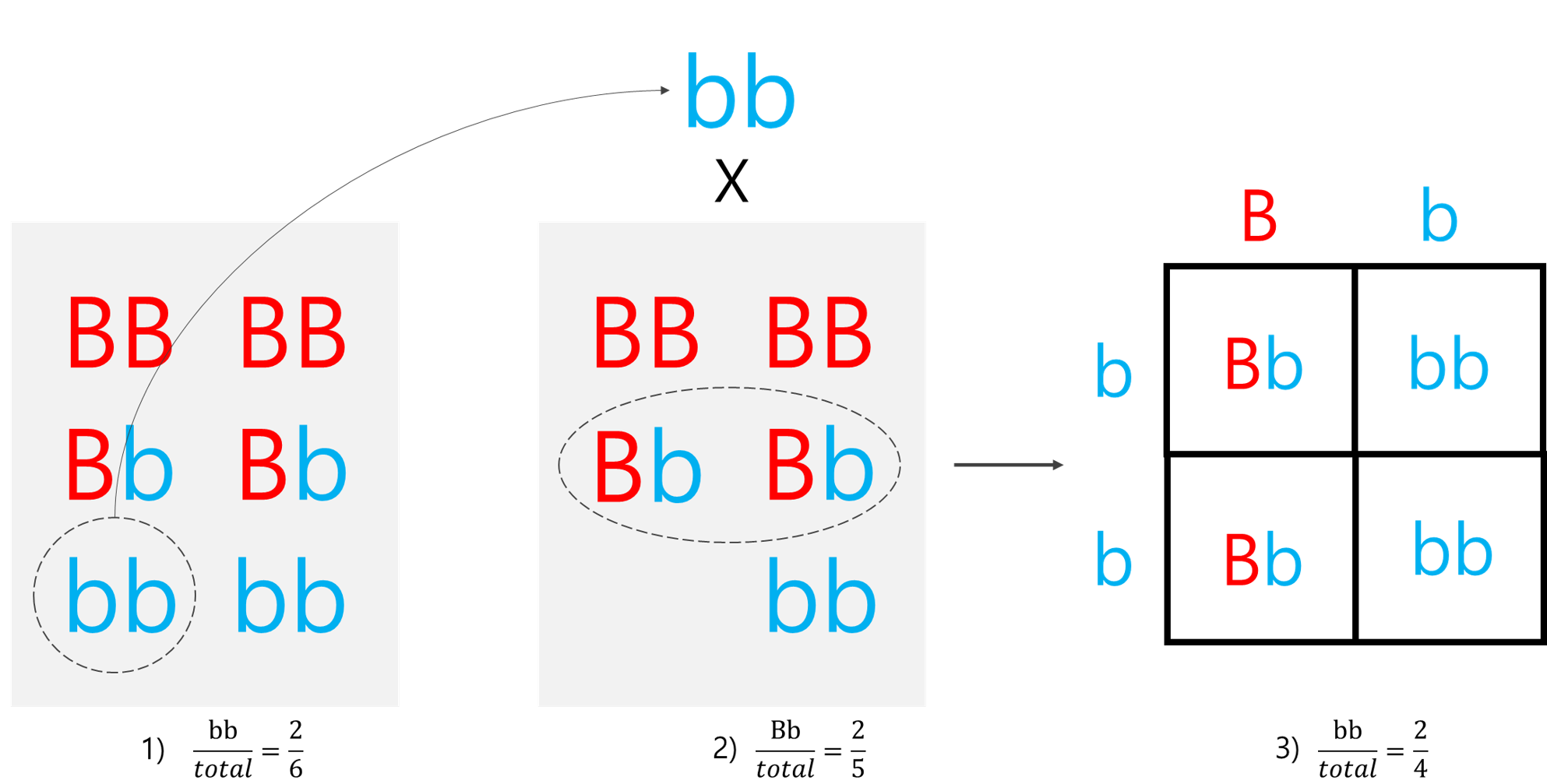
일단 bb를 먼저 선택하는 경우(bbXBb)과, Bb를 먼저 선택하는 경우(BbXbb) 총 2가지가 존재 한다
각 확률은 2/6*2/5*2/4 = 4/60 -> 총 2가지 경우가 있으니 8/60
다 더해보자
BbXBb에서 bb의 확률 1/60.. + BbXbb의에서 bb의 확률 8/60 + bbXbb의에서 bb의 확률 4/60 = 13/60 = 0.2166666..
즉, Bb와 BB가 나타날 확률은 1- 0.2166666.. = 0.78333..가 나온다.
풀이
with open('./rosalind/rosalind_iprb.txt', 'r') as f :
pop = f.read().split()
k, m , n= map(int,pop[0::])
total = k+m+n
total_cases = total*(total-1)*4
prob_aa = 0
## Aa - Aa
if m > 1 :
m_to_aa = m*(m-1)*1
# Aa-aa
if m > 1 and n>1:
mn_to_aa = n*m*2*2
# aa-aa
if n > 1 :
n_to_aa = n*(n-1)*4 # 8
prob_aa = m_to_aa + mn_to_aa + n_to_aa
round((1-prob_aa/total_cases), 5)
추천수 많은 풀이를 참고해서 정리해 보자면, 여기서 k는 total을 구할때 빼고는 쓸 일이 없다.
또한 m, n>1조건도 설정할 필요가 없다. 어차피 0이라면 곱해서도 0 이 나오기 때문이다.
1-(m*(m-1) + (n*m*2*2) + (n*(n-1)*4))/(4*total*(total-1))즉 분모는 m*(m-1) + (n*m*2*2) + (n*(n-1)*4)
분자는 4*total*(total-1) 로 두면 된다
조금 정리해 보면 [n*m + n(n-1) + m(m-1)/4]/total(total-1) 로 정리가 가능 하다
즉 아래와 같이 정리할 수 있다
1-(m*(m-1)/4 + n*m + n*(n-1)) / (total*(total-1))
