2023.06.07 R풀이 추가

Wascally Wabbits
1202년, 피보나치로 알려진 피사의 레오나르도가 Liber Abaci책을 출간하면서 번식에 대한 문제를 담았다. 토끼 번식에 대한 가정은 아래와 같다.
- 인구는 1월 1일 한 쌍의 신생아 토끼에서 시작한다.
- 한 달이 지나면 생식 연령에 도달한다.
- 특정 달에는 모든 토끼는 생식 연령의 다른 토끼와 짝을 이룬다.
- 정확히 두 토끼의 짝짓기 한달 후, 암컷과 수컷 토끼 총 한 쌍을 낳는다.
- 토끼는 죽거나 번식을 멈추지 않는다.
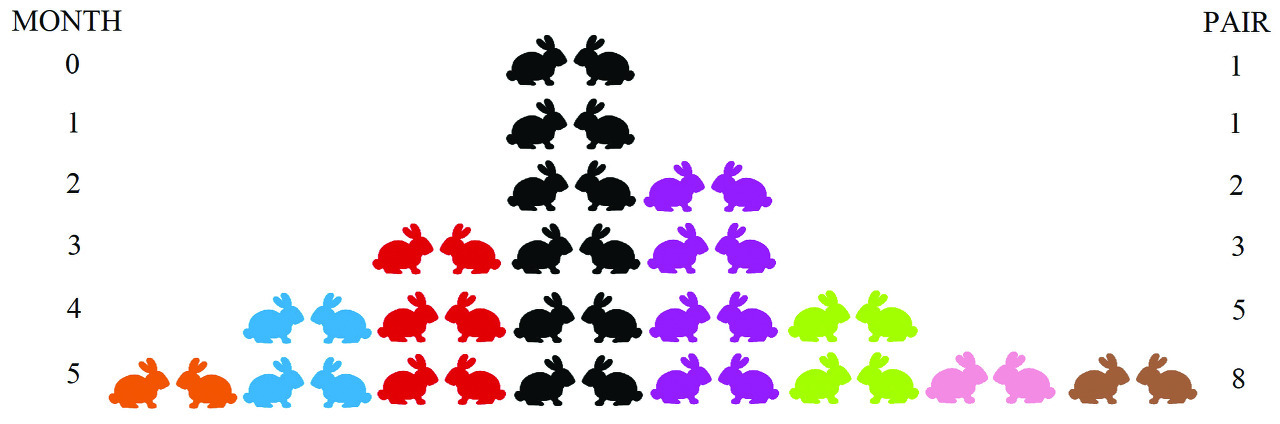
Fn은 각 달에 총 토끼 짝의 수라고 했을 때, F3 = F2 + F1 = 2 + 1 = 3이다
Fibonacci's exercise은 1년이 지난 후 몇 쌍의 토끼가 남는지에 대한 계산을 했다. 1년 후 개체수는 144쌍에 이른다.
비록 토끼의 불멸(immortality) 이 가정되어 현실성이 없어 보이지만, 실제로 토끼는 호주에서 많은 식물종을 근절시키고 초원을 사막화하였다.
| 문제
수열(sequence)이란 반복되어 정렬된 수를 말한다. 수열은 무한일 수도, 유한일 수도 있다.
두 수열의 예시를 보자. 유한수열은 이와 같고 -> (π,√(2), 0,π) 무한수열은 이와 같다 ->(1,3,5,7,9,…).
우리는 a_n을 n개의 수열을 가졌다고 정의하겠다.
$$ a_{n} $$
재귀식(점화식; recurrence relation)이란 반복 해서 현재 값이 이전값을 반영하는 식을 말한다. 파보나치 토끼 수열의 경우, n 번째 달의 토끼 수는 이전 달에 살아있던 토끼와 새로 생성된 자손 토끼를 모두 포함한다. 중요하게 관찰해야 하는 점은 n번째 달의 자손의 수는 두 달 전에 살아 있던 토끼의 수와 같다는 것이다.
결과적으로, F_n(n번째 달의 총토끼의 수) = F_(n-1) + F_(n-2)을 만족한다. (수열의 처음은 이와 같다 -> F1 = F2 = 1)
Given : 양의 정수 n≤40 , k≤5
Return : 첫 달은 1쌍의 토끼부부에서 시작되며, 1달이 세대주기이다. 즉 한 달이 지나면 생식이 가능한 토끼가 된다. 또한 생식연령이 된 다음달에는 자손 k 쌍을 낳는다. n 번째 달이 지난 후에 총 토끼의 수를 반환해라.
| 데이터와 결과
Sample Dataset
5 3
Sample Output
19
예제 문제 풀이
이 문제는 데이터에서 어떠한 규칙을 찾고, 그 규칙의 방정식을 만들어 코드를 작성하는 것이다.
일단 무식하게 손수 계산을 해보자.
첫 번째 달과 두 번째 달은 각각 한 쌍만이 존재한다.
두 번째 달에 짝짓기를 하고, 세 번째 달에 총 3쌍의 토끼를 출산한다. 각 쌍은 암컷과 수컷으로 구성되어 있다. 넷째 달에는 이미 생식연령을 넘긴 한 쌍만이 다시 3쌍을 출산하고, 생식연령에 다른 3쌍은 짝짓기를 한다.다섯 번째 달은 다시 기존 한 쌍이 또 3쌍을 출산하고, 이전에 생식연령을 넘긴 3쌍이 각 3쌍을 출산한다. 그림으로 그려보면 아래와 같다.
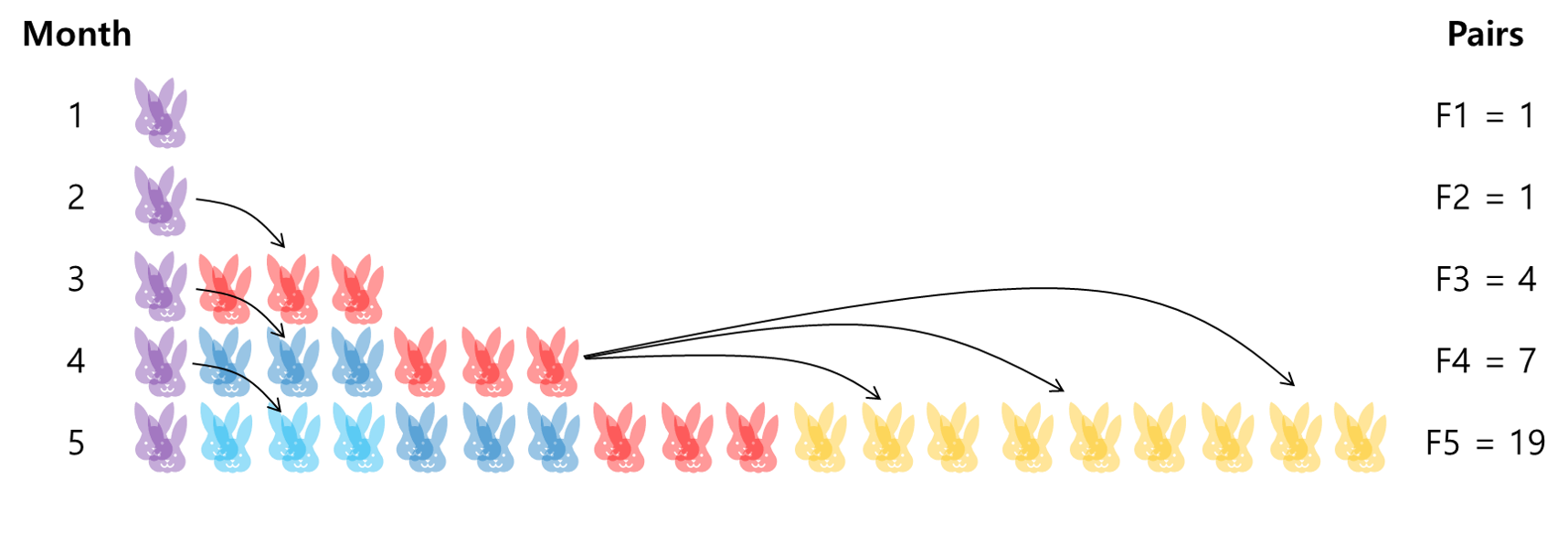
그렇다면 F6은 무슨 값일까? 답은 40이다.
F5에서 생식가능한 쌍은 총 1+3+3 임으로 총 7쌍이다.
기존 19개체에 생식 가능한 쌍에 7 개체가 각 3쌍을 낳으면, 6달에 존재하는 총 토끼 쌍은 19 + 21 = 22쌍이다.
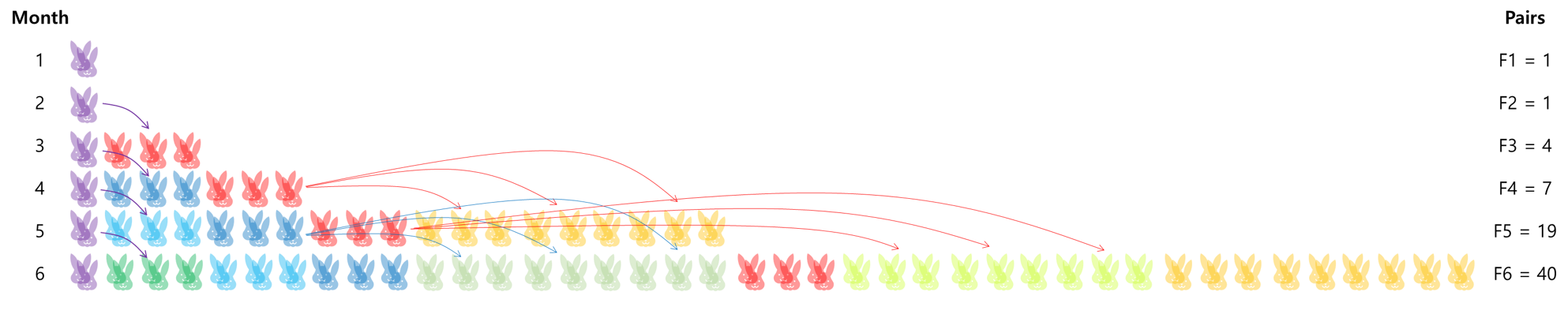
이를 보면 F6 = F5 + F3*3 = 19 + 7*3 = 40
이를 공식화해보면, F_n = F(n-1)+ F(n-2)*k 이다.
| Python
with open('./rosalind_fib.txt', 'r') as f :
X = f.read().split()
n, k = map(int,X[0::])
def recurr(n):
if n==1 or n==2:
return 1
else:
return recurr(n-1) + recurr(n-2)*k
recurr(n)
| R
일단 R에서 재귀식을 써본게 너무 오래되서 다시 책을 봤다.
6.2 재귀함수(Recursive function) | 통계 프로그래밍 언어
2023년도 1학기 정보통계학과 통계 프로그래밍 언어 강의 노트로 해당 노트: https://zorba78.github.io/cnu-r-programming-lecture-note/
zorba78.github.io
Python과 크게 다를바는 없다.
k = 3
recurr <- function(n) {
if (n %in% c(1,2) ) return(1) # 종료 조건
return(recurr(n-1) + recurr(n-2)*k)
}
recurr(5) # 19
